Welcome back (again)!
For those of you who are just joining us, this is the third part of the “be-a-maze-d” series.
You can find the
first part here and the
second part here.
If you are ready to dive in, let’s get started!
A different approach for the solving code
In the parts 1 and 2 we wrote our code in 2 big functions, one for generating the maze and one for solving it. Let’s remember the function that solves the maze that we wrote in the first part:
def solve_maze(maze, startX, startY, endX, endY):
visited = []
for x, line in enumerate(maze):
visited.append([])
for cell in line:
visited[x].append(cell)
visited[startX][startY] = 3
currX = startX
currY = startY
options = []
while currX != endX or currY != endY:
if currX+1 < len(maze[currX]) and maze[currX+1][currY] != 1 and visited[currX+1][currY] < 2:
options.append(Point(currX+1, currY))
if currX-1 >= 0 and maze[currX-1][currY] != 1 and visited[currX-1][currY] < 2:
options.append(Point(currX-1, currY))
if currY+1 < len(maze[currX]) and maze[currX][currY+1] != 1 and visited[currX][currY+1] < 2:
options.append(Point(currX, currY+1))
if currY-1 >= 0 and maze[currX][currY-1] != 1 and visited[currX][currY-1] < 2:
options.append(Point(currX, currY-1))
if len(options) == 0: # no options means nowhere to go
return None
go_to_point = options.pop()
currX = go_to_point.x
currY = go_to_point.y
visited[currX][currY] = 2
visited[endX][endY] = 4
return visited
As you can see, this function is quite long and has a lot of nested if statements. Let’s try to use object oriented programming to make this code more readable and easier to understand.
So, basically our code will more or less do the same as before but we’ll put it in a class and break down the functionality into smaller methods.
The class definition starts like this:
class MazeSolver:
def __init__(self):
self.currX = 0
self.currY = 0
self.intersections = []
You can see that our class has an intersections property. That’s already a hint for the approach we’ll take.
Next, just like in the first function we’ll need to initialize the visited array:
...
def _init_visited(self):
self.visited = []
for x, line in enumerate(self.maze.matrix):
self.visited.append([])
for cell in line:
self.visited[x].append(cell)
You can see that I made init_visted a private method, so the calling code would not care about this part.
Now, let’s see what we need to check for every option:
- Would it hit a wall?
- Would it hit a visited cell?
- Would it be out of bounds?
Instead of checking all of these conditions in nested if statements we’ll create a private function for each.
...
def _is_not_visited(self, x, y):
return self.visited[x][y] < 2
def _is_not_wall(self, x, y):
return self.maze.matrix[x][y] != 1
def _is_in_bounds(self, x, y):
return x >= 0 and x < len(self.maze.matrix[x]) and y >= 0 and y < len(self.maze.matrix)
Now we can combine those private methods in another private method called can_go.
This method will return True if the point is not a wall, not visited and in bounds.
...
def _can_go(self, x, y):
return self._is_in_bounds(x, y) and self._is_not_wall(x, y) and self._is_not_visited(x, y)
Looks much nicer, right?
Let’s take a look at our older implementation and talk about how they are different.
if currX+1 < len(maze[currX]) and maze[currX+1][currY] != 1 and visited[currX+1][currY] < 2:
options.append(Point(currX+1, currY))
if currX-1 >= 0 and maze[currX-1][currY] != 1 and visited[currX-1][currY] < 2:
options.append(Point(currX-1, currY))
if currY+1 < len(maze[currX]) and maze[currX][currY+1] != 1 and visited[currX][currY+1] < 2:
options.append(Point(currX, currY+1))
if currY-1 >= 0 and maze[currX][currY-1] != 1 and visited[currX][currY-1] < 2:
options.append(Point(currX, currY-1))
- Repetition! We can see that those nested ifs look alike.
- No separation of concerns. The logic for checking the conditions is mixed with the logic for adding the options to the stack.
- Readability. It’s a bit hard to understand from just looking and the code.
In the new implementation it’s:
- Reusable so we can stay DRY.
- Encapsulated. So we can change or add logic without affecting the rest of the code.
- Readable. We can easily read that we are checking if the code
can_goand also what are the terms.
Now, we can use the can_go method to see our options for walking to the next cell of the maze.
...
def _get_options(self, x, y):
options = [(x-1, y), (x+1, y), (x, y-1), (x, y+1)]
return [option for option in options if self._can_go(option[0], option[1])]
You can see that instead of a bunch of if statements we have a list of tuples and a one liner filtered list. This is definitely much nicer, but you can argue that it’s not as readable as using a few if statements. In general one liners are not as readable as a few lines of code, you have to really take a moment and look closely. Also, the tuples in the list are not so nice looking.
If you are a stickler for readability you can do something like this:
...
def _left(self, x, y):
return (x-1, y)
def _right(self, x, y):
return (x+1, y)
def _up(self, x, y):
return (x, y+1)
def _down(self, x, y):
return (x, y-1)
def _get_options(self, x, y):
directions = [self._left, self._right, self._up, self._down]
result = []
for direction in directions:
if self._can_go(direction(option[0], option[1])):
result.append(option)
return result
My choice would be the first one, but it’s a matter of taste. Reducing 15 lines of code to 2 is not always a good idea, but it works for me here.
Great! now that we have our options we can start walking to the next cell.
The _walk method will return True if we can walk to the next cell and False if we can’t.
Note that we are checking whether we are at an intersection and if we are we are adding it to the intersections list.
The intersections list replaces our stack from the first implementation.
...
def _walk(self):
self.visited[self.currX][self.currY] = 2
options = self._get_options(self.currX, self.currY)
print('options: ', options)
if len(options) == 0:
return False
elif len(options) > 1:
self.intersections.append((self.currX, self.currY))
self.currX, self.currY = options.pop()
return True
In our first implementation we used a stack and we were adding all options to it. In this implementation we are only adding the intersections, because those are actually the only cells we care about. And of course after talking about intersections, we need to be able to get back to the last one.
...
def _go_to_last_intersection(self):
if len(self.intersections) == 0:
return False
last_intersection = self.intersections.pop()
self.currX = last_intersection[0]
self.currY = last_intersection[1]
return True
Ok! We now have all the small pieces that we need in order to solve the maze.
Now, for the final part - the solve method.
...
def solve(self):
while self.currX != self.maze.endX or self.currY != self.maze.endY:
can_walk = self._walk()
if not can_walk:
can_go_to_last_intersection = self._go_to_last_intersection()
if can_go_to_last_intersection:
continue
return None # We cannot walk and have nowehere to go back to
self.visited[self.maze.startX][self.maze.startY] = 3
self.visited[self.maze.endX][self.maze.endY] = 4
return self.visited
Alright, great! This looks much better than our first implementation.
Let’s take a look at the entire class:
class MazeSolver:
def __init__(self):
self.currX = 0
self.currY = 0
self.intersections = []
def init_maze(self, maze):
self.maze = maze
self.currX = maze.startX
self.currY = maze.startY
self._init_visited()
def _init_visited(self):
self.visited = []
for x, line in enumerate(self.maze.matrix):
self.visited.append([])
for cell in line:
self.visited[x].append(cell)
def _is_not_visited(self, x, y):
return self.visited[x][y] < 2
def _is_not_wall(self, x, y):
return self.maze.matrix[x][y] != 1
def _is_in_bounds(self, x, y):
return x >= 0 and x < len(self.maze.matrix[x]) and y >= 0 and y < len(self.maze.matrix)
def _can_go(self, x, y):
return self._is_in_bounds(x, y) and self._is_not_wall(x, y) and self._is_not_visited(x, y)
def _get_options(self, x, y):
options = [(x-1, y), (x+1, y), (x, y-1), (x, y+1)]
return [option for option in options if self._can_go(option[0], option[1])]
def _walk(self):
self.visited[self.currX][self.currY] = 2
options = self._get_options(self.currX, self.currY)
print('options: ', options)
if len(options) == 0:
return False
elif len(options) > 1:
self.intersections.append((self.currX, self.currY))
self.currX, self.currY = options.pop()
return True
def _go_to_last_intersection(self):
if len(self.intersections) == 0:
return False
last_intersection = self.intersections.pop()
self.currX = last_intersection[0]
self.currY = last_intersection[1]
return True
def solve(self):
while self.currX != self.maze.endX or self.currY != self.maze.endY:
can_walk = self._walk()
if not can_walk:
can_go_to_last_intersection = self._go_to_last_intersection()
if can_go_to_last_intersection:
continue
return None # We cannot walk and have nowehere to go back to
self.visited[self.maze.startX][self.maze.startY] = 3
self.visited[self.maze.endX][self.maze.endY] = 4
return self.visited
You can now use this class instead of the old function (not much different).
def main():
size = 40
maze = generate_maze(size)
while maze == None:
maze = generate_maze(size)
# use our new MazeSolver class to solve maze
# and return the solved maze
maze_solver = MazeSolver()
maze_solver.init_maze(maze)
solved = maze_solver.solve()
if solved == None:
print("Can't solve maze")
return
print_maze(solved)
I know that I should be using the _property to mark private properties. But I didn’t want so many underscores in the blog post. Probably if this was a real project with other people involved, it would have been full of those ugly underscores.
So, our solving code is now organized, lean and clean. What about our generation code? It’s still a big ugly beast.. Actually it’s much worse than the solving code. Let’s see if we can do something about it.
Refactoring the generation code
There are few things we want to improve in our generation code.
- We had a problem with the maze sometimes not being able to generate.
- The maze sometimes had too many blank spaces that made very wide paths.
- The code only went one step at a time making the paths very short.
The approach we’ll take here is to try to “walk” a random number steps at a time at a random direction. Also, instead of just reaching the end and stop, we will exhaust the options for paths in the maze. Another change would be to make the end less likely to have two paths to it.
Let’s see how we can do that.
You probably already guessed by the solving code that we are doing this more Object Oriented..
So, we will start by creating a new class called MazeGenerator.
class MazeGenerator:
def init_maze(self, size, max_path_len=10):
self.size = size
self.max_path_len = max_path_len
self.maze = []
self.track = []
for i in range(0, size):
self.maze.append([])
for j in range(0, size):
self.maze[i].append(1)
Note that we added a new parameter max_path_len which is the maximum length of a path (the max number of random step in a direction).
The track property is like the stack we used in the old code. But now it’s “track”.. I like the name better.
Like the MazeSolver class, we start by creating a few private methods.
This is how we determine the start and ending points.
...
def _create_starting_and_ending_points(self):
self.startX = 1
self.startY = 1
self.endX = 1
self.endY = 1
while self.startX == self.endX or self.startY == self.endY or abs(self.startX - self.endX) < (self.size/2) or abs(self.startY - self.endY) < (self.size/2):
random.seed()
self.startX = random.randint(1, self.size-2)
self.startY = random.randint(1, self.size-2)
self.endX = random.randint(1, self.size-2)
self.endY = random.randint(1, self.size-2)
Looks just like the code we had before, but now it’s a private method of the class.
Let’s add now the code for checking that we are in bounds and not destroying walls.
...
def _is_in_bounds(self, x, y):
return x >= 1 and x < self.size - 1 and y >= 1 and y < self.size -1
def _is_not_destroying_wall(self, x, y):
options = [(x+1, y), (x-1, y), (x, y+1), (x, y-1)]
num_of_zeros = 0
for option in options:
if self.maze[option[0]][option[1]] == 0:
num_of_zeros += 1
return num_of_zeros <= 1
Great! We can now write the method _can_walk_to which will check if we can walk to a given point.
...
def _can_walk_to(self, x, y):
return self._is_in_bounds(x, y) and self._is_not_destroying_wall(x, y) and self.maze[x][y] != 0
Note that we are also checking for self.maze[x][y] != 0 because we don’t want to walk to a point we already visited.
Now for direction randomization. Slightly different than we used before.
Instead of using currX and currY and just increment them we’ll use lambdas.
...
def _randomize_direction(self):
left = lambda: (self.currX - 1, self.currY)
right = lambda: (self.currX + 1, self.currY)
up = lambda: (self.currX, self.currY + 1)
down = lambda: (self.currX, self.currY - 1)
directions = [left, right, up, down]
options = []
for direction in directions:
x, y = direction()
if self._can_walk_to(x, y):
options.append(direction)
if len(options) == 0:
return None
random.seed()
return options[random.randint(0, len(options)-1)]
Ok, what’s going on here? Each lambda will make the current point advance in a direction, so instead of just giving us the next point it will give us a reusable function that we can call a few times. Why is that good you ask? You’ll see in a minute. After the lambdas we check which directions we can walk to and add them to a list of options. Then we pick a random direction from the list and return it.
Now for the actual walking.
...
def _try_walk(self, num_of_steps):
steps_taken = 0
direction = self._randomize_direction()
if direction is None:
return steps_taken
for i in range(0, num_of_steps):
x, y = direction()
if self._can_walk_to(x, y):
self.maze[x][y] = 0
self.currX = x
self.currY = y
self.track.append((x, y))
steps_taken += 1
return steps_taken
As you can see the function takes a num_of_steps which is the number of steps the function will try to walk.
This addresses the issue we mentioned earlier, and will hopefully make the maze more nice looking.
Another private method for backtracking, just for more readability:
...
def _go_back(self):
self.currX, self.currY = self.track.pop()
Not really necessary but makes the generation code a bit more clear.
And now, for the generation code!
...
def generate(self):
self._create_starting_and_ending_points()
self.currX = self.startX
self.currY = self.startY
self.maze[self.currX][self.currY] = 0
self.track.append((self.currX, self.currY))
while len(self.track) > 0:
random.seed()
num_of_steps = random.randint(1, self.max_path_len)
steps_taken = self._try_walk(num_of_steps)
if steps_taken == 0:
self._go_back()
self.maze[self.startX][self.startY] = 3
self.maze[self.endX][self.endY] = 4
return Maze(self.maze, self.startX, self.startY, self.endX, self.endY)
Alrighty! So you can basically read what the code is doing.
It starts with creating the starting and ending points, then it starts walking.
It will try to walk num_of_steps steps, and if it can’t it will backtrack.
You can see that we are now using while len(self.track) > 0: as our stopping condition.
This will only stop the generation when the whole maze is full of paths and walls.
Another addition is a better print_maze function. I added numbers, some more spacing and an animate ability that we can see later.
Here is the new function:
def print_maze(maze, clear=False):
print('')
print('')
print(' ', end='')
for i in range(len(maze[0])):
print("{0:0=2d}".format(i), '', end='')
print('')
rows = 3
for i, line in enumerate(maze):
print(' ', "{0:0=2d}".format(i) ,' ', end='')
for cell in line:
if cell == 1:
print(colored('## ', 'red'), end='')
elif cell == 0:
print(' ', end='')
elif cell == 3:
print('@@ ', end='')
elif cell == 4:
print('&& ', end='')
else:
print(colored('** ', 'green'), end='')
print('\n', end='')
rows += 1
print('')
print('')
rows += 2
if clear:
for i in range(0, rows):
sys.stdout.write("\033[K") # remove line
sys.stdout.write("\033[1A") # up the cursor
It’s basically the same with slight improvements.
Now let’s see how the maze generated maze looks like.
This is our main function:
def main():
size = 40
maze_generator = MazeGenerator()
maze_generator.init_maze(size, max_path_len=10)
maze = maze_generator.generate()
if maze == None:
print("Can't generate maze")
return
print_maze(maze.matrix)
You can see that the ending point (marked with &&) is just in the middle of a path. That’s a bit ugly and I said we’ll fix it.
So let’s do that.
What we’ll do is, in case the walking code walks next to the ending point, it will just go there and return a 0 for steps_taken.
That will actually create some sort of a dead end, because it will walk to it and then the calling code would backtrack to the latest point in the track list.
Let’s see the checking method:
...
def _is_near_ending(self, x, y):
options = [(x+1, y), (x-1, y), (x, y+1), (x, y-1)]
for option in options:
_x, _y = option
if _x == self.endX and _y == self.endY:
return True
Pretty straightforward, we just check if the current point is next to the ending point.
And now for the improved _try_walk method:
...
def _try_walk(self, num_of_steps):
steps_taken = 0
direction = self._randomize_direction()
if direction is None:
return steps_taken
for i in range(0, num_of_steps):
if self._is_near_ending(self.currX, self.currY): # <- new code
self.currX = self.endX
self.currY = self.endY
self.maze[self.currX][self.currY] = 0
return 0
x, y = direction()
if self._can_walk_to(x, y):
self.maze[x][y] = 0
self.currX = x
self.currY = y
self.track.append((x, y))
steps_taken += 1
return steps_taken
Cool! Let’s see a maze generated with this new addition.
And another example:
Let’s have a look at the entire class.
class MazeGenerator:
def init_maze(self, size, max_path_len=10):
self.size = size
self.max_path_len = max_path_len
self.maze = []
self.track = []
for i in range(0, size):
self.maze.append([])
for j in range(0, size):
self.maze[i].append(1)
def _create_starting_and_ending_points(self):
self.startX = 1
self.startY = 1
self.endX = 1
self.endY = 1
while self.startX == self.endX or self.startY == self.endY or abs(self.startX - self.endX) < (self.size/2) or abs(self.startY - self.endY) < (self.size/2):
random.seed()
self.startX = random.randint(1, self.size-2)
self.startY = random.randint(1, self.size-2)
self.endX = random.randint(1, self.size-2)
self.endY = random.randint(1, self.size-2)
def _is_in_bounds(self, x, y):
return x >= 1 and x < self.size - 1 and y >= 1 and y < self.size -1
def _is_not_destroying_wall(self, x, y):
options = [(x+1, y), (x-1, y), (x, y+1), (x, y-1)]
num_of_zeros = 0
for option in options:
if self.maze[option[0]][option[1]] == 0:
num_of_zeros += 1
return num_of_zeros <= 1
def _can_walk_to(self, x, y):
return self._is_in_bounds(x, y) and self._is_not_destroying_wall(x, y) and self.maze[x][y] != 0
def _is_near_ending(self, x, y):
options = [(x+1, y), (x-1, y), (x, y+1), (x, y-1)]
for option in options:
_x, _y = option
if _x == self.endX and _y == self.endY:
return True
def _randomize_direction(self):
left = lambda: (self.currX - 1, self.currY)
right = lambda: (self.currX + 1, self.currY)
up = lambda: (self.currX, self.currY + 1)
down = lambda: (self.currX, self.currY - 1)
directions = [left, right, up, down]
options = []
for direction in directions:
x, y = direction()
if self._can_walk_to(x, y):
options.append(direction)
if len(options) == 0:
return None
random.seed()
return options[random.randint(0, len(options)-1)]
def _try_walk(self, num_of_steps):
steps_taken = 0
direction = self._randomize_direction()
if direction is None:
return steps_taken
for i in range(0, num_of_steps):
if self._is_near_ending(self.currX, self.currY):
self.currX = self.endX
self.currY = self.endY
self.maze[self.currX][self.currY] = 0
return 0
x, y = direction()
if self._can_walk_to(x, y):
self.maze[x][y] = 0
self.currX = x
self.currY = y
self.track.append((x, y))
steps_taken += 1
return steps_taken
def _go_back(self):
self.currX, self.currY = self.track.pop()
def generate(self):
self._create_starting_and_ending_points()
self.currX = self.startX
self.currY = self.startY
self.maze[self.currX][self.currY] = 0
self.track.append((self.currX, self.currY))
while len(self.track) > 0:
random.seed()
num_of_steps = random.randint(1, self.max_path_len)
steps_taken = self._try_walk(num_of_steps)
if steps_taken == 0:
self._go_back()
self.maze[self.startX][self.startY] = 3
self.maze[self.endX][self.endY] = 4
return Maze(self.maze, self.startX, self.startY, self.endX, self.endY)
Cool cool cool, good looking, clean, readable code.
Still quite a bit of code to read, but it’s enough to read the
generatemethods to get the gist of it. We don’t really need to read the entire code in order to understand what’s happening. That is a huge thing actually.
People usually say “Yeah sure, it’s my code I’ll be able to understand it..”, but they are wrong. You’ll be able to understand it after a month (maybe), but not after a year. This way it’s even better other people will be able to understand it after a year, without you having to explain it to them.
Let’s see if everything works together.
Solving the maze
Our main function will now look like this:
def main():
size = 40
maze_generator = MazeGenerator()
maze_generator.init_maze(size, max_path_len=10)
maze = maze_generator.generate()
if maze == None:
print("Can't generate maze")
return
maze_solver = MazeSolver()
maze_solver.init_maze(maze)
solved = maze_solver.solve()
if solved == None:
print("Can't solve maze")
return
print_maze(solved)
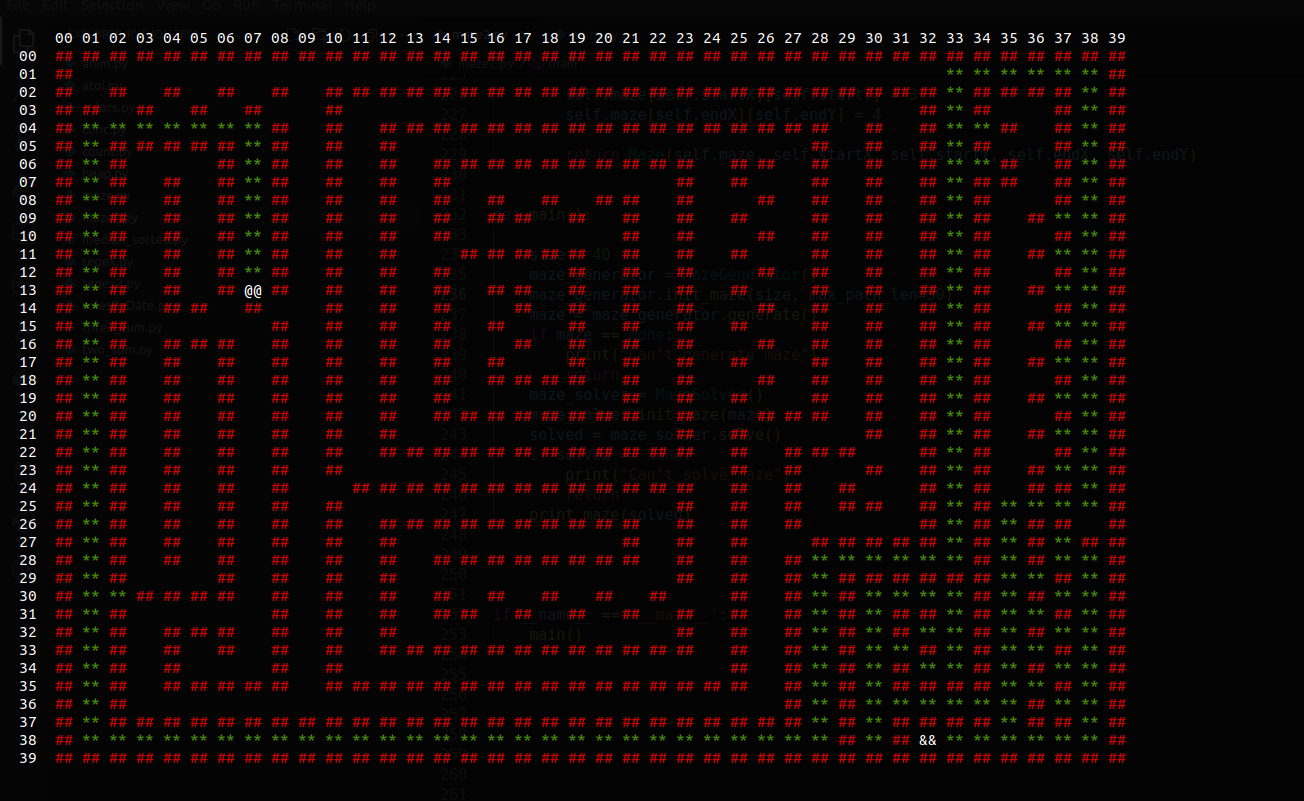
And there we go! A solved maze!
You can play with max_len_path and see how it affects the paths.
Here is a maze with max_len_path=2:
And this is with max_len_path=30:
Some animation please
I thought it would be cool to kind of animate the maze as it’s being solved.
If you look at print_maze function, you’ll see that there’s a clear option.
Like this:
...
if clear:
for i in range(0, rows):
sys.stdout.write("\033[K") # remove line
sys.stdout.write("\033[1A") # up the cursor
This actually clears the terminal screen, and moves the cursor up. So, we can print the maze again and create some sort of really bad animation (Hey at least I tell it like it is).
Now we have to plant the printing code in the solve method.
Yes, I know it’s putting in irrelevant code in the solving method and it’s not considered good separation of concerns.
All that is true. But here’s a real life pragmatic situation for you: “People want to see animation, and they want to see it NOW”.
That’s life some times :)
Let’s see our hacky little animation:
...
def solve(self, animate=False): # New parameter here
while self.currX != self.maze.endX or self.currY != self.maze.endY:
if animate: # New if statement here
print_maze(self.visited, clear=True)
time.sleep(0.1)
can_walk = self._walk()
if not can_walk:
can_go_to_last_intersection = self._go_to_last_intersection()
if can_go_to_last_intersection:
continue
self.visited[self.maze.startX][self.maze.startY] = 3
self.visited[self.maze.endX][self.maze.endY] = 4
print_maze(self.visited)
return None # We cannot walk and have nowehere to go back to
self.visited[self.maze.startX][self.maze.startY] = 3
self.visited[self.maze.endX][self.maze.endY] = 4
return self.visited
And there it is:
Pretty nice, right?
Conclusion
So this concludes our maze solving adventure. We took a simple maze solving algorithm, wrote some functional messy code and then refactored it to be more readable and understandable. We also added some animation to make it more fun.
I hope you enjoyed it, and learned something new.
As always, you can find the code on Github. So feel free to play with it and see what happens.
If you liked it, please share it with your friends and colleagues. Thanks for reading!